线段树 HDU 1556 Color the ball

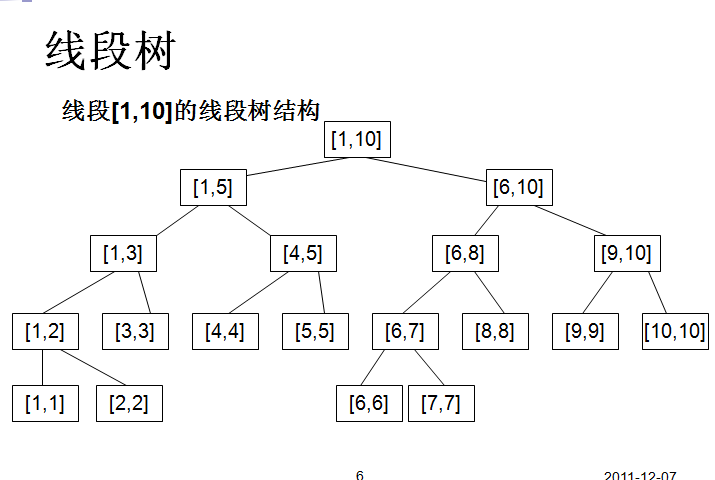
线段树

擅长处理区间，可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN)。而未优化的空间复杂度为2N，实际应用时一般还要开4N的数组以免越界，因此有时需要离散化让空间压缩。

线段树

Description

N个气球排成一排，从左到右依次编号为1,2,3….N.每次给定2个整数a b(a <= b),lele便为骑上他的“小飞鸽”牌电动车从气球a开始到气球b依次给每个气球涂一次颜色。但是N次以后lele已经忘记了第I个气球已经涂过几次颜色了，你能帮他算出每个气球被涂过几次颜色吗？

Input

每个测试实例第一行为一个整数N,(N <= 100000).接下来的N行，每行包括2个整数a b(1 <= a <= b <= N)。当N = 0，输入结束。

Output

每个测试实例输出一行，包括N个整数，第I个数代表第I个气球总共被涂色的次数。

Sample Input

Sample Output

1 1 1

3 2 1

啥也不说了，~~都在酒里，~~ 都在代码里。

Code

#include <cstdio>
#include <iostream>
using namespace std;
const int N = 100005;

struct node
{
    int L, R;
    int val;
} a[N * 4];

///对于三个函数中的l 、r
///init: l、r是分割时被 “固定” 划分的区间
///update与query：l、r是操作时外界“自由”给出的区间
///初始化
void init(int num, int l, int r)///num为从根到叶的区间排号
{
    ///初始化当前区间
    a[num].L = l;
    a[num].R = r;
    a[num].val = 0;

    if(l == r)///区间长度到1后退出
        return ;

    ///递归初始化子区间
    int mid = (l + r) / 2;
    init(num * 2, l, mid);
    init(num * 2 + 1, mid + 1, r);
}

///更新(排号为num的、以l为左界以r为右界的区间的val)
void update(int num, int l, int r)
{
    if(a[num].L == l && a[num].R == r)
    {
        a[num].val++;///针对此题val加一，其他题视题意而定
        return ;
    }

    if(a[num].L == a[num].R)///都找到"点"了，还没找到区间
        return ;

    int mid = (a[num].L + a[num].R) / 2;
    ///当前查找区间 的中值 在 目标区间 的右侧，去左孩子找
    if(mid >= r)
        update(num * 2, l, r);
    ///当前查找区间 的中值 在目标区间 的左侧
    else if(mid < l)///注意！这里没有等号！这里没有等号！
        update(num * 2 + 1, l, r);
    ///当前查找区间 的中值 在目标区间 里！
    else
    {
        update(num * 2, l, mid);
        update(num * 2 + 1, mid + 1, r);
    }
}

int query(int num, int l, int r)
{
    if(a[num].L == l && a[num].R == r)
        return a[num].val;
    if(a[num].L == a[num].R)
        return 0;
    int mid = (a[num].L + a[num].R) / 2;
    if(mid >= r)
        return a[num].val + query(num * 2, l, r);
    else if(mid < l)
        return a[num].val + query(num * 2 + 1, l, r);
    else
        return a[num].val + query(num * 2, l, mid) + query(num * 2 + 1, mid + 1, r);
}

int main()
{
    int n;
    while(cin >> n && n)
    {
        init(1, 1, n);
        for(int i = 0; i < n; ++i)
        {
            int a, b;
            cin >> a >> b;
            update(1, a, b);
        }
        for(int i = 1; i <= n; ++i)
            printf("%d%c", query(1, i, i), i == n ? '\n': ' ');
    }
    return 0;
}