归并排序

归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

归并过程为：比较a[i]和a[j]的大小，若a[i]≤a[j]，则将第一个有序表中的元素a[i]复制到r[k]中，并令i和k分别加上1；否则将第二个有序表中的元素a[j]复制到r[k]中，并令j和k分别加上1，如此循环下去，直到其中一个有序表取完，然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。归并排序的算法我们通常用递归实现，先把待排序区间[s,t]以中点二分，接着把左边子区间排序，再把右边子区间排序，最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。

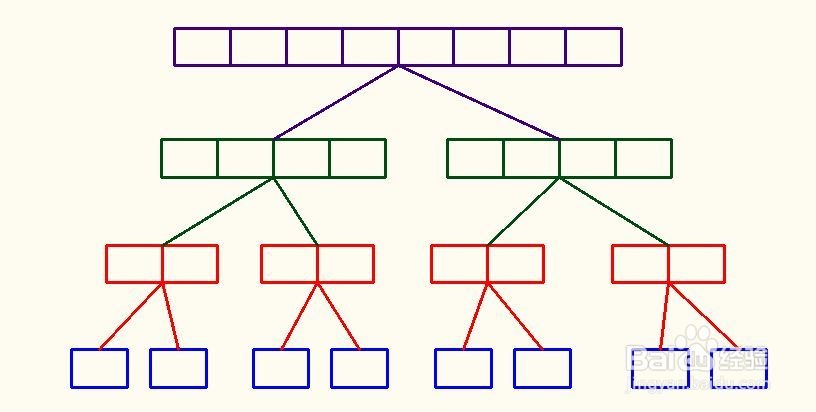
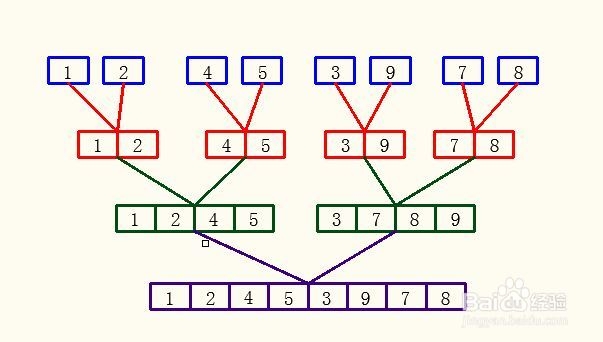
原理示意

先将数据分开排序，然后再合并起来，最后形成一个排好的序列。

Code of MERGE-SORT

#include <cmath>
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100;

int fr[N];
int bk[N];

///合并两个排好序的序列
void my_merge(int * s, int start, int mid, int over)
{
    int fr_len = mid - start + 1;
    int bk_len = over - mid;

    for(int i = 0; i < fr_len; ++i)
        fr[i] = s[start + i];
    for(int i = 0; i < bk_len; ++i)
        bk[i] = s[mid + 1 + i];

    ///两个序列中的数相互比较，将较小的数先插入新的序列中
    int i = 0, j = 0, k = start;
    while(i < fr_len && j < bk_len)
    {
        if(fr[i] < bk[j])
            s[k++] = fr[i++];
        else
            s[k++] = bk[j++];
    }

    ///剩余元素合并
    while(i < fr_len)
        s[k++] = fr[i++];
    while(j < bk_len)
        s[k++] = bk[j++];
}

void merge_sort(int * s, int start, int over)
{
    if(start < over)
    {
        int mid = (start + over) / 2;
        merge_sort(s, start, mid);
        merge_sort(s, mid + 1, over);
        my_merge(s, start, mid, over);
    }
}

int main()
{
    int s[] = {9, 4, 5, 7, 3, 6, 8, 2, 0, 1};
    int len = sizeof(s) / sizeof(int);
    int ans[len];
    merge_sort(s, 0, len - 1);
    for(int i = 0; i < len; ++i)
        cout << s[i] << ' ';
    cout << '\n';
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

Code of 探索过程版

#include <cmath>
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100;

int fr[N];
int bk[N];

///合并两个排好序的序列
void my_merge(int * s, int start, int mid, int over)
{
    int fr_len = mid - start + 1;
    int bk_len = over - mid;
    cout << "前部分长度 " << fr_len << " 后部分长度 " << bk_len << '\n';

    for(int i = 0; i < fr_len; ++i)
        fr[i] = s[start + i];
    for(int i = 0; i < bk_len; ++i)
        bk[i] = s[mid + 1 + i];

    cout << "前部分元素" << '\n';
    for(int i = 0; i < fr_len; ++i)
        cout << fr[i] << ' ';
    cout << '\n';
    cout << "后部分元素" << '\n';
    for(int i = 0; i < bk_len; ++i)
        cout << bk[i] << ' ';
    cout << '\n';

    ///两个序列中的数相互比较，将较小的数先插入新的序列中
    int i = 0, j = 0, k = start;
    while(i < fr_len && j < bk_len)
    {
        cout << i << ' ' << fr[i] << ' ' << j << ' ' << bk[j] << '\n';
        if(fr[i] < bk[j])
            s[k++] = fr[i++];
        else
            s[k++] = bk[j++];
    }

    ///剩余元素合并
    while(i < fr_len)
        s[k++] = fr[i++];
    while(j < bk_len)
        s[k++] = bk[j++];

    cout << "此次排序结果 ： " << '\n';
    for(int t = 0; t < k; ++t)
        cout << s[t] << ' ';
    cout << '\n';
}

void merge_sort(int * s, int start, int over)
{
    if(start < over)
    {
        int mid = (start + over) / 2;
        merge_sort(s, start, mid);
        merge_sort(s, mid + 1, over);
        my_merge(s, start, mid, over);
    }
}

int main()
{
    int s[] = {9, 4, 5, 7, 3, 6, 8, 2, 0, 1};
    int len = sizeof(s) / sizeof(int);
    int ans[len];
    merge_sort(s, 0, len - 1);
    for(int i = 0; i < len; ++i)
        cout << s[i] << ' ';
    cout << '\n';
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76