SDNUOJ 1089 拓扑排序

Description

给定一个有向图，若图无环，则将其进行拓扑排序并输出，否则输出IMPOSABLE。

Input

第一行为两个整数n(1<=n<=1000)、m(1<=m<=100000)； 之后m行，每行两个整数a、b(0 < a, b <= n)表示一条从a到b的有向边。

Output

若存在环，输出IMPOSABLE，否则输出一行用一个空格隔开的拓扑排序的结果，若存在多个结果，输出字典序最小的。

Sample Input(自写)

5 3
2 5
2 4
1 3
4 4
1 2
2 3
3 4
4 1

Sample Output

1 2 3 4 5

IMPOSABLE

做题过程

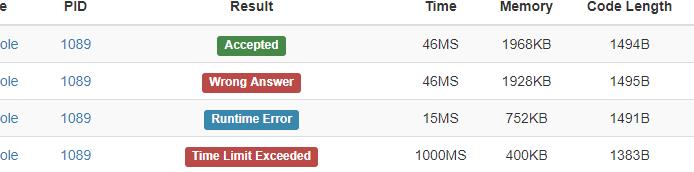
原来的判环与输出结果都没问题，但要输出字典序最小的！我想了个办法：

邻接表存的时候按顺序放:

            cin >> a >> b;
            v[a].insert(lower_bound(v[a].begin(), v[a].end(), b), b);

但TLE了

用priority_queue一点点存：

RE了：

把模板搬过来没改数据范围，改完了交上

WA了：

对拍发现：有环时输出IMPOSABLE(可实施的、可强制的)而不是IMPOSSIBLE(不可能的)

最后AC了。

Code

#include <queue>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

int n, m;
int in[1005];
vector<int> ans;
vector<int> v[100005];

bool bfs(priority_queue< int, vector<int>, greater<int> > q)
{
    int sum = 0;
    while(q.size())
    {
        int tem = q.top();
        ans.push_back(tem);
        sum++;
        q.pop();

        for(int i = 0; i < v[tem].size(); ++i)
        {
            in[ v[tem][i] ]--;
            if(!in[ v[tem][i] ])
                q.push(v[tem][i]);
        }
    }
    return sum == n;
}

int main()
{
//    freopen("00in.txt", "r", stdin);
    while(cin >> n >> m)
    {
        priority_queue< int, vector<int>, greater<int> > q;
        memset(in, 0, sizeof(in));
        ans.clear();
        for(int i = 0; i <= n; ++i)
            v[i].clear();

        int a, b;
        for(int i = 1; i <= m; ++i)
        {
            cin >> a >> b;
//            v[a].insert(lower_bound(v[a].begin(), v[a].end(), b), b);
            v[a].push_back(b);
            in[b]++;
        }

        for(int i = 1; i <= n; ++i)///1 ~ n
            if(!in[i])
                q.push(i);
        if(!bfs(q))
            cout << "IMPOSABLE" << '\n';
        else
        {
            int sz = ans.size();
            for(int i = 0; i < sz; ++i)
                printf("%d%c", ans[i], i == sz - 1 ? '\n' : ' ');
        }
    }
    return 0;
}