矩阵快速幂与斐波那契不得不说的故事

矩阵快速幂

求矩阵A的k（较大）次幂（% 1e9 + 7）

Code(模板)

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

typedef long long ll;
const int mod = 1e9 + 7;
ll n, mi;

struct mtx
{
    ll m[105][105];
};

mtx mpy(mtx a, mtx b)
{
    mtx ans;
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= n; ++j)
        {
            ans.m[i][j] = 0;
            for(int k = 1; k <= n; ++k)
                ans.m[i][j] = (ans.m[i][j] + a.m[i][k] * b.m[k][j]) % mod;
        }
    return ans;
}

mtx fast_mod(mtx a, ll k)
{
    mtx ans = a;
    k--;
    while(k)
    {
        if(k & 1)
            ans = mpy(ans, a);
        a = mpy(a, a);
        k >>= 1;
    }
    return ans;
}

int main()
{
    mtx a;
    scanf("%lld%lld", &n, &mi);
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= n; ++j)
            scanf("%lld", &a.m[i][j]);
    if(mi == 0)
    {
        for(int i = 1; i <= n; ++i)
            for(int j = 1; j <= n; ++j)
                ans.m[i][j] = (i == j ? 1 : 0);
    }
    else
        ans = fast_mod(a, mi);
    for(int i = 1; i <= n; ++i)
    {
        for(int j = 1; j <= n; ++j)
        {
            cout << ans.m[i][j];
            if(j != n)
                cout << ' ';
        }
        cout << '\n';
    }
    return 0;
}

SDNUOJ 1062 Fibonacci

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

typedef long long ll;
const int mod = 1e9 + 7;

ll n, mi;
struct mtx
{
    ll m[10][10];
};

mtx mpy(mtx a, mtx b)
{
    mtx ans;
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= n; ++j)
        {
            ans.m[i][j] = 0;
            for(int k = 1; k <= n; ++k)
                ans.m[i][j] = (ans.m[i][j] + a.m[i][k] * b.m[k][j]) % mod;
        }
    return ans;
}

mtx fast_mod(mtx a, ll k)
{
    mtx ans = a;
    k--;
    while(k)
    {
        if(k & 1)
            ans = mpy(ans, a);
        a = mpy(a, a);
        k >>= 1;
    }
    return ans;
}

int main()
{
    n = 2;
    mtx a;
    a.m[1][1] = 1, a.m[1][2] = 1, a.m[2][1] = 1, a.m[2][2] = 0;
    scanf("%lld", &mi);
    if(mi == 0)
        cout << '0' << '\n';
    else
    {
        a = fast_mod(a, mi);
        cout << a.m[1][2] << '\n';
    }
    return 0;
}

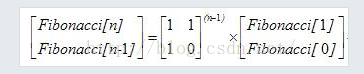
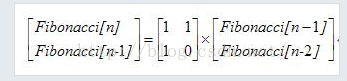
对于此题

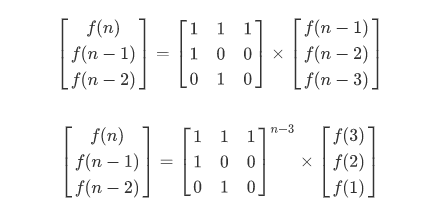
SDNUOJ 1085 爬楼梯再加强版

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

typedef long long ll;
const int mod = 1e9 + 7;

ll n, mi;
struct mtx
{
    ll m[10][10];
};

mtx mpy(mtx a, mtx b)
{
    mtx ans;
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= n; ++j)
        {
            ans.m[i][j] = 0;
            for(int k = 1; k <= n; ++k)
                ans.m[i][j] = (ans.m[i][j] + a.m[i][k] * b.m[k][j]) % mod;
        }
    return ans;
}

mtx fast_mod(mtx a, ll k)
{
    mtx ans = a;
    k--;
    while(k)
    {
        if(k & 1)
            ans = mpy(ans, a);
        a = mpy(a, a);
        k >>= 1;
    }
    return ans;
}

int main()
{
    n = 3;
    mtx a, b;
    a.m[1][1] = 1, a.m[1][2] = 1, a.m[1][3] = 1;
    a.m[2][1] = 1, a.m[2][2] = 0, a.m[2][3] = 0;
    a.m[3][1] = 0, a.m[3][2] = 1, a.m[3][3] = 0;
    b.m[1][1] = 4, b.m[2][1] = 2, b.m[3][1] = 1;
    scanf("%lld", &mi);
    if(mi == 1)
        cout << '1' << '\n';
    else if(mi == 2)
        cout << '2' << '\n';
    else if(mi == 3)
        cout << '4' << '\n';
    else
    {
        a = fast_mod(a, mi - 3);
        a = mpy(a, b);
        cout << a.m[1][1] << '\n';
    }
    return 0;
}