阿里巴巴协助征战SARS(困难)

Description

你需要统计所有满足下列条件的长度为 n 的字符串的个数:

1. 字符串仅由 A、T、C、G 组成

2. A和C 出现偶数次(也可以不出现)

   数据范围：n <= 10的（10的5次幂）

https://nanti.jisuanke.com/t/38352

Idea

数据小的时候，正常用矩阵快速幂

数据大了，先用欧拉降幂预处理

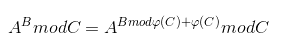
这里B % C, B是string类型读入的大数，所以用一下大数求余

Code

#include <map>
#include <cmath>
#include <queue>
#include <vector>
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;
#define ll long long

//欧拉函数
ll phi(ll n)
{
     ll i, rea = n;
     for(i = 2; i * i <= n; ++i)
         if(n % i == 0)
         {
             rea = rea - rea / i;
             while(n % i == 0)
                 n /= i;
          }
     if(n > 1)
         rea = rea - rea / n;
     return rea;
}


const int mod = 1e9 + 7;

struct mtx
{
    ll m[105][105];
};

int n = 3;
ll mi;

mtx mpy(mtx a, mtx b)
{
    mtx ans;
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= n; ++j)
        {
            ans.m[i][j] = 0;
            for(int k = 1; k <= n; ++k)
                ans.m[i][j] = (ans.m[i][j] + a.m[i][k] * b.m[k][j]) % mod;
        }
    return ans;
}

mtx fast_mod(mtx a, ll k)
{
    mtx ans = a;
    k--;
    while(k)
    {
        if(k & 1)
            ans = mpy(ans, a);
        a = mpy(a, a);
        k >>= 1;
    }
    return ans;
}

int main()
{
    ll tem = phi(mod);
    string s;
    mtx a;
    a.m[1][1] = 2, a.m[1][2] = 1, a.m[1][3] = 0;
    a.m[2][1] = 2, a.m[2][2] = 2, a.m[2][3] = 2;
    a.m[3][1] = 0, a.m[3][2] = 1, a.m[3][3] = 2;
    while(cin >> s)
    {
        if(s[0] == '0')
            break;
        mi = 0;
        int sz = s.size();
        for(int i = 0; i < sz; ++i)//大数求余
            mi = ((mi * 10) % tem + (s[i] - '0') % tem) % tem;
        mi += tem;
        mtx ans = fast_mod(a, mi);
        cout << ans.m[1][1] << '\n';
    }
    return 0;
}