POJ 3281 Dining(最大流最小割)

Description

农夫为他的 N (1 ≤ N ≤ 100) 牛准备了 F (1 ≤ F ≤ 100)种食物和 D (1 ≤ D ≤ 100) 种饮料。每头牛都有各自喜欢的食物和饮料，而每种食物或饮料只能分配给一头牛。最多能有多少头牛可以同时得到喜欢的食物和饮料？

Analyze

不可以二分图匹配，因为牛要匹配两种东西，求其跟每种东西的最大匹配，取交集也不是，取并集也不是，需建模用最大流解决

1. 多源点、多汇点要建立超源点、超汇点

2. 牛置于中间，左放食物右放饮料（或反过来）

3. 连线权值为1，求最大流即答案

   要注意：中间的牛要拆点

关于拆点

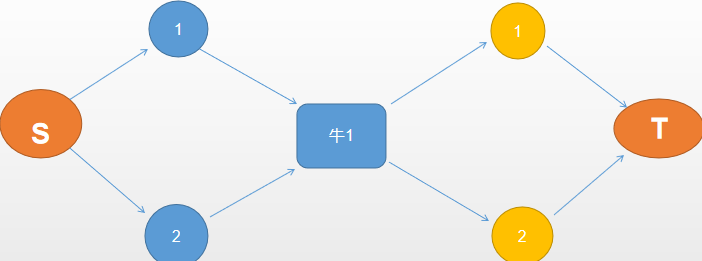
很明显,一头牛同时匹配了多种食物饮料,最大流是2,但答案是1(只满足了一头牛)

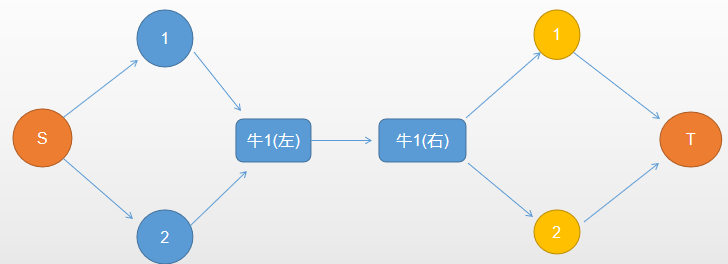
限流：限制流经每头牛的流量最大为1

Code

#include <set>
#include <map>
#include <stack>
#include <queue>
#include <ctime>
#include <cmath>
#include <cstdio>
#include <vector>
#include <bitset>
#include <string>
#include <cstring>
#include <sstream>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <functional>
#define eps 1e-8
#define PI acos(-1.0)
#define ll long long
using namespace std;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
#define Close ios::sync_with_stdio(false);

void Debug(char * s)
{
    cout << "-------------  " << s << "  -------------" << '\n';
}
const int N = 1005;

int n;///网络流中最重要的是建模构图，其中全局变量总点数n要计算清楚
int maxflow, deep[N];

struct edge
{
    int from, to, w, pre;
} a[N * N];

queue<int> q;
int cnt = -1;
int head[N], cur[N];

void add(int from, int to, int w)
{
    a[++cnt].to = to;
    a[cnt].from = from;
    a[cnt].pre = head[from];
    a[cnt].w = w;
    head[from] = cnt;
}

bool bfs(int s, int t)
{
    memset(deep, INF, sizeof(deep));
    while(!q.empty())
        q.pop();
    for(int i = 0; i <= n; ++i)
        cur[i] = head[i];
    deep[s] = 0;
    q.push(s);

    while(!q.empty())
    {
        int first = q.front();
        q.pop();
        for(int i = head[first]; ~i; i = a[i].pre)
        {
            if(deep[ a[i].to ] == INF && a[i].w)///w在此处用来做标记 是正图还是返图
            {
                deep[ a[i].to ] = deep[first] + 1;
                q.push(a[i].to);
            }
        }
    }
    if(deep[t] < INF)
        return 1;
    return 0;
}

int dfs(int now, int t, int limit)
{
    if(!limit || now == t)
        return limit;
    int flow = 0, f;
    for(int i = cur[now]; ~i; i = a[i].pre)
    {
        cur[now] = i;
        if(deep[ a[i].to ] == deep[now] + 1)
            if(f = dfs(a[i].to, t, min(limit, a[i].w)))
            {
                flow += f;
                limit -= f;
                a[i].w -= f;
                a[i ^ 1].w += f;
                if(!limit)
                    break;
            }
    }
    return flow;
}

///bfs分层，dfs增广、处理残余网络、反向边

void Dinic(int s, int t)
{
    int temp;
    while(bfs(s, t))
    {
        while((temp = dfs(s, t, INF)) > 0)
            maxflow += temp;
    }
}

int main()
{
    memset(head, -1, sizeof(head));
    int nn, ff, dd;
    scanf("%d%d%d", &nn, &ff, &dd);
    n = 2 * nn + ff + dd + 2;
    for(int i = 1; i <= ff; ++i)
    {
        add(0, i, 1);
        add(i, 0, 0);
    }
    for(int i = 1; i <= dd; ++i)
    {
        add(i + 2 * nn + ff, 1 + dd + 2 * nn + ff, 1);
        add(1 + dd + 2 * nn + ff, i + 2 * nn + ff, 0);
    }
    int num_f = 0, num_d = 0, idx = 0;
    for(int i = 1; i <= nn; ++i)
    {
        scanf("%d%d", &num_f, &num_d);
        for(int j = 1; j <= num_f; ++j)
        {
            scanf("%d", &idx);
            add(idx, i + ff, 1);
            add(i + ff, idx, 0);
        }
        for(int j = 1; j <= num_d; ++j)
        {
            scanf("%d", &idx);
            add(i + nn + ff, idx + 2 * nn + ff, 1);
            add(idx + 2 * nn + ff, i + nn + ff, 0);
        }
        add(i + ff, i + nn + ff, 1);
        add(i + nn + ff, i + ff, 0);
    }
    Dinic(0, 1 + dd + 2 * nn + ff);
    cout << maxflow << '\n';
    return 0;
}

1. n（总点数）的计算出错了

2. 添边时超级源点0写成了1

3. i为序号写成了idx(idx在其他地方做过序号)

   所以要分清“同类”