POJ 3169 Layout(最短路解差分约束)

Description

N头牛(1~N)按序号排成一排

L个最大距离限制：某两头牛至多相距某个距离

D个最小距离限制：某两头牛至少相距某个距离

求第一头牛与第n头牛之间的最大距离

差分约束系统

如果一个系统由n个变量和m个约束条件组成，

形成m个形如 ai - aj ≤ k 的不等式(i,j∈[1,n],k为常数),

则称其为差分约束系统

举例

给定n个变量和m个不等式，

每个不等式的形式为 x[i] - x[j] <= a[k] (0 <= i, j < n, 0 <= k < m， a[k]已知)，

求 x[i] - x[j] 的最大值。

例如当n = 4，m = 5，给出如下图所示的不等式组，求x3 - x0的最大值

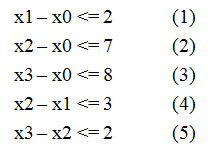
观察x3 - x0的性质，我们如果可以通过不等式的两两加和得到c个形如 x3 - x0 <= Ti 的不等式，那么 min{ Ti | 0 <= i < c } 就是我们要求的x3 - x0的最大值

x3 - x0 <= 8 (3)

x3 - x0 <= 9 (2)+(5)

x3 - x0 <= 7 (1)+(4)+(5)

要同时满足，答案取7

求差分约束系统转为求单源最短路

x[i] - x[j] <= a[k]

令dis[i] = x[i]，令i = v， j = u， a[k] = w(j, i)

dis[v] - dis[u] <= w(u, v)
-> dis[v] <= dis[u] + w(u, v)

似最短路

前L条边：
    dis[v] - dis[u] <= w(u, v)
    add(u, v, w);
后D条边：
    dis[v] - dis[u] >= w(u, v)
    统一采用 <= (两边同乘 -1)
    dis[u] - dis[v] <= - w(u, v)
    add(v, u, -w);
隐藏边：
    dis[i + 1] - dis[i] >= 0
    dis[i] - dis[i + 1] <= 0
    add(i + 1, i, 0);

相应转化后，要求1到n最大距离

最大对应到题目上，（L个）每个最大距离都取等号，才能对应“最大”

那为什么是求最短路(最小距离)呢？

x3 - x0 <= 8

x3 - x0 <= 9

x3 - x0 <= 7

这里多条路只能选最短的那条（因为要同时满足三个不等式），这就对应起来了

补充

存在负环：dis[n]可无限小， -1

图不连通：dis[n] == INF， -2

Code

#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1005;
const int inf = 0x3f3f3f3f;

struct node///存放“边”
{
    int from, to, w, pre;
} a[N * N << 1];

int head[N], cnt, dis[N], times[N], tot, sum, n, L, D;
bool vis[N];///vis[i]：0表示i不在队列里，1表示i在队列里

void init()///受n影响，应安排在n被赋值之后
{
    cnt = 0;
    for(int i = 0; i <= n; ++i)
        dis[i] = inf, times[i] = 0, vis[i] = 0, head[i] = -1;
    return ;
}

void add(int from, int to, int w)
{
    a[cnt].from = from;
    a[cnt].to = to;
    a[cnt].w = w;
    a[cnt].pre = head[from];
    head[from] = cnt;
    cnt++;
}

bool spfa(int start)
{
    deque<int> q;
    dis[start] = 0;///到自己的距离为0
    vis[start] = 1;
    q.push_front(start);
    tot = 1, sum = 0;
    while(q.size())
    {
        int first = q.front();
        q.pop_front();
        vis[first] = 0;
        tot--;
        sum -= dis[first];

        for(int i = head[first]; ~ i; i = a[i].pre)
        {
            int t = a[i].to;
            if(dis[t] > dis[first] + a[i].w)
            {
                dis[t] = dis[first] + a[i].w;
                if(!vis[t])
                {
                    vis[t] = 1;         ///极值优化             ///平均值优化
                    if(q.empty() || dis[t] > dis[q.front()] || dis[t] * tot >= sum)
                        q.push_back(t);
                    else
                        q.push_front(t);
                    sum += dis[t];
                    tot++;
                    if(++times[t] > n)
                        return 0;
                }
            }
        }
    }
    return 1;
}

int main()
{
    scanf("%d%d%d", &n, &L, &D);
    init();
    int u, v, w;
    for(int i = 0; i < L; ++i)
    {
        scanf("%d%d%d", &u, &v, &w);
        add(u, v, w);
    }
    for(int i = 0; i < D; ++i)
    {
        scanf("%d%d%d", &u, &v, &w);
        add(v, u, -w);
    }
    for(int i = 1; i < n; ++i)
        add(i + 1, i, 0);
    if(spfa(1))
    {
        if(dis[n] == inf)
            cout << "-2" << '\n';
        else
            cout << dis[n] << '\n';
    }
    else
        cout << "-1" << '\n';
    return 0;
}

部分原文来自：

http://www.cppblog.com/menjitianya/archive/2015/11/19/212292.html

https://blog.csdn.net/my_sunshine26/article/details/72849441