2019 ICPC Asia Nanchang Regional

E.Bob’sProblem

N个点（从1到N）

M条边（带权，有黑白两种）

选边，使得在图联通的前提下，边权和最大

限制条件：白边不能超过K条

analyze

1.黑边没有限制数目，又是求最大边权和，所以选择所有黑边

2.(无向图可用并查集缩点)缩点后，对于白边，求最大生成树

3.若有多余白边(在K的限制下)，贪心选取权值大的

细节：①int node = n;每次连入一个点node—，若最后node>1不能生成树输出-1.②每次用一条白边k—，若最后k<0白边不够用输出-1.③求生成树过程中未用到的白边单独存一数组中，若最后k>0则sort后贪心选.

有点东西：这题里，无向图求缩点，和 求生成树，都用了并查集

Code

#include <cmath>
#include <cstdio>
#include <string>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define ll long long

const int maxn = 50005;
const int maxm = 500005;

struct edge
{
    ll u, v, w;
    bool operator < (const edge t) const
    {
        return w > t.w;
    }
};

edge white[maxm];
edge black[maxm];
edge other[maxm];
ll pre[maxn];

ll found(ll x)
{
    return x == pre[x] ? x : pre[x] = found(pre[x]);
}

int main()
{
    int _;
    scanf("%d", &_);
    while(_--)
    {
        ll n, m, k, u, v, w, c, ans = 0, b_num = 0, w_num = 0, o_num = 0;
        scanf("%lld %lld %lld", &n, &m, &k);
        for(ll i = 0; i < m; ++i)
        {
            scanf("%lld %lld %lld %lld", &u, &v, &w, &c);
            if(c == 0)
            {
                black[b_num].u = u;
                black[b_num].v = v;
                black[b_num].w = w;
                b_num++;
            }
            else
            {
                white[w_num].u = u;
                white[w_num].v = v;
                white[w_num].w = w;
                w_num++;
            }
        }

        ///选择所有的黑边 + 并查集缩点(无向图)
        for(ll i = 0; i <= n; ++i)
            pre[i] = i;
        ll node = n;
        for(ll i = 0; i < b_num; ++i)
        {
            ll x = found(black[i].u);
            ll y = found(black[i].v);
            if(x != y)
            {
                pre[x] = y;
                node--;
            }
            ans += black[i].w;
        }

        ///Kruskal最大生成树
        sort(white, white + w_num);
        for(ll i = 0; i < w_num; ++i)
        {
            ll x = found(white[i].u);
            ll y = found(white[i].v);
            if(x != y)
            {
                pre[x] = y;
                node--, k--;
                ans += white[i].w;
            }
            else
                other[o_num++] = white[i];
        }

        if(node > 1 || k < 0)
            cout << "-1" << '\n';
        else
        {
            sort(other, other + o_num);
            for(ll i = 0; i < k && i < o_num; ++i)
                ans += other[i].w;
            cout << ans << '\n';
        }
    }
    return 0;
}

C.And and Pair

给出一个大数N的二进制表示，找出有多少有序对(i, j)满足以下条件

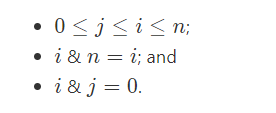
analyze

1.i >= j

2.n的0位，i在该位上也必须是0

3.i的1位，j在该位上必须是0(这也说明i > j)

于是，针对n，先确定i，再根据i确定j

①我们先看 i 与 j 的关系：

针对某个 i ，将其最高位1前导0去掉后，剩x个0， j 就有种

因为 j 在 i 的每个0位上可选0或1

②再来看 n 推 i 推 j ：

从低位到高位看（从右向左），（因为从左向右不好算）

找到1所在位，若它右边有 y 个1，x 个0，推导总结得方案数：

又有公式

得方案数:

Code

#include<bits/stdc++.h>
using namespace std;
const int mod = int(1e9 + 7);
#define ll long long

/// i >=  j
/// n 的 0 位, i 在该位上也必须是0
/// i 的 1 位, j 在该位上必须是0 (i > j)

ll num2[100005];
ll num3[100005];

int main()
{
    int _;
    scanf("%d", &_);
    num3[0] = num2[0] = 1;
    for(int i = 1; i <= 100001; ++i)
    {
        num2[i] = num2[i - 1] * 2 % mod;
        num3[i] = num3[i - 1] * 3 % mod;
    }
    while(_--)
    {
        string s;
        cin >> s;
        ll ans = 0;
        int len = s.length(), zero = 0, one = 0;
        for(int i = len - 1; i >= 0; --i)
        {
            if(s[i] == '1')
            {
                ans = (ans + (num2[zero] * num3[one] % mod)) % mod;
                one++;
            }
            else
                zero++;
        }
        ans = (ans + 1) % mod;
        cout << ans << '\n';
    }
    return 0;
}

G.Eating Plan

N个数字（1~N的排列），Q组询问

某个数字的阶乘 代表 那堆食物的 重量

必须连续进食（吃第3、5堆则必须吃第4堆）

肚子里攒 998857459 就减去它(这个地方是在说取模)

询问 K ，最少吃几堆，才能使肚子里的食物不少于K

analyze

凡涉及 阶乘取模 ，想想是不是到哪一个数字就成0了，此后都是0

这个模数998857459是合数，更有可能，打表发现在2803项是这样的

①预处理 前2802的阶乘

②RMQ离线处理询问（不过这个RMQ的处理方法，是通解吗？）

Code

#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define ll long long
const ll maxn = 100005;
const ll mod = 998857459;

ll num[maxn];
ll fac[maxn];
ll sum[maxn];
ll ans[maxn];

ll cnt;
struct node
{
    ll val, id;
} rec[maxn];

int main()
{
    fac[0] = 1;
    for(ll i = 1; i <= 3000; ++i)
    {
        fac[i] = fac[i - 1] * i % mod;
        if(fac[i] == 0)
        {
            ///cout << i << '\n';///2803
            break;
        }
    }

    ll n, m;
    scanf("%lld %lld", &n, &m);
    for(ll i = 1; i <= n; ++i)
    {
        scanf("%lld", &num[i]);
        num[i] = fac[ num[i] ];
    }

    for(ll i = 1; i <= n; ++i)
        if(num[i])
        {
            cnt++;
            rec[cnt].id = i;
            rec[cnt].val = num[i];
//            sum[cnt] = (sum[cnt - 1] + num[i]) % mod;
            sum[cnt] = (sum[cnt - 1] + num[i]);
        }

    for(ll i = 1; i <= cnt; ++i)
        for(ll j = i; j <= cnt; ++j)
            ans[ rec[j].id - rec[i].id + 1 ] = max(ans[ rec[j].id - rec[i].id + 1 ], (sum[j] - sum[i - 1]) % mod);

    while(m--)
    {
        ll q, len = -1;
        scanf("%lld", &q);
        for(ll i = 1; i <= n; ++i)
            if(ans[i] >= q)
            {
                len = i;
                break;
            }
        if(len == -1)
            puts("-1");
        else
            cout << len << '\n';
    }
    return 0;
}