HDU 4725 The shortest Path in Nya Graph

Description

N个点分别落在各层(layer), 每层可能有多个点, 也可能没有点, 每一层和其上下两层之间的点权值为C。另外有M条权值为w的边, 求1到N的最短路径, 如果不存在输出 -1

Analyze

如果N个点均匀落在相邻两层上，那么连线是N ^ 2级别的，会TLE

优化：每层设立一个层节点，(i + n)表示第i层的层节点标号

层节点指向本层所有节点，权值为0

本层所有节点指向相邻层的层节点，权值为w

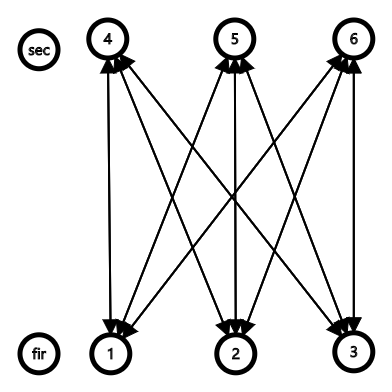
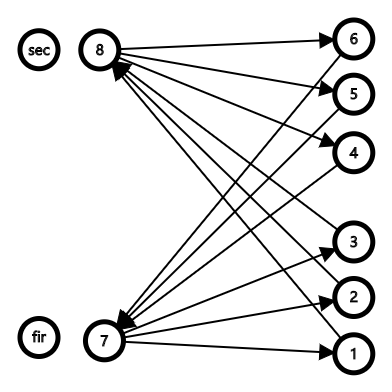
上图例子中，优化前18条单向边，优化后12条

添加层节点消耗了空间，换取了时间

另外，Dijkstra堆优化真好用，用过即AC(好过stack实现的spfa)

还有，Dijkstra堆优化存图时用vector+pair

Code

#include <queue>
#include <stack>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 100105;
const int inf = 0x3f3f3f3f;

typedef pair<int, int> P;
vector<P> node[2 * N];

int layer[2 * N], head[2 * N], cnt, dis[2 * N], tot, sum, n, m, c;
bool vis[2 * N];

void init()
{
    cnt = 0;
    for(int i = 0; i <= n + n; ++i)
        dis[i] = inf, vis[i] = 0, node[i].clear(), layer[i] = 0;
}

void Dijkstra()
{
    priority_queue<P, vector<P>, greater<P> > q;
    dis[1] = 0;
    q.push(P(dis[1], 1));
    while(!q.empty())
    {
        P now = q.top();
        q.pop();
        int idx = now.second;
        if(vis[idx])
            continue;
        vis[idx] = 1;
        int sz = node[idx].size();
        for(int i = 0; i < sz; ++i)
        {
            P nxt = node[idx][i];
            if(dis[nxt.second] > dis[idx] + nxt.first)
            {
                dis[nxt.second] = dis[idx] + nxt.first;
                q.push(P(dis[nxt.second], nxt.second));
            }
        }
    }
}

int main()
{
    int t, tot = 1;
    scanf("%d", &t);
    while(t--)
    {
        scanf("%d%d%d", &n, &m, &c);
        init();
        for(int i = 1; i <= n; ++i)
            scanf("%d", &layer[i]);


        for(int i = 1; i <= n; ++i)///traverse each node instead of each layer
        {
            node[ layer[i] + n ].push_back(P(0, i));
            if(layer[i] > 1)
                node[i].push_back(P(c, layer[i] + n - 1));
            if(layer[i] < n)
                node[i].push_back(P(c, layer[i] + n + 1));
        }

        int u, v, w;
        for(int i = 1; i <= m; ++i)
        {
            scanf("%d %d %d", &u, &v, &w);
            node[u].push_back(P(w, v));
            node[v].push_back(P(w, u));
        }
        cout << "Case #" << tot++ << ": ";
        Dijkstra();
        if(dis[n] != inf)
            cout << dis[n] << '\n';
        else
            cout << "-1" << '\n';
    }
    return 0;
}