POJ 1151 Atlantis(Segment Tree about Scanning lines)

Description

求N个矩形面积的并集

扫描线

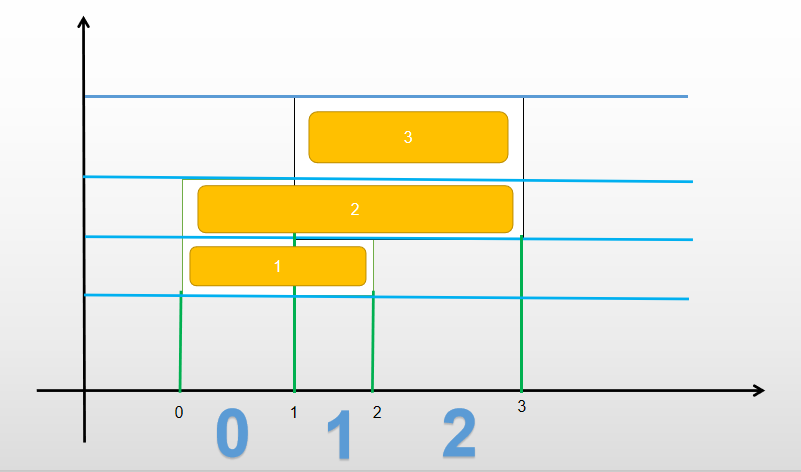
Scanning Lines

线段树是可以从0开始的，只是保证标号从1开始就行

线段树每个点维护一段区间

当然需要离散化，将浮点数类型的x值对应成每条垂线的标号，这样之后可以用线段树维护当前扫描线的长度，计算具体长度时逆离散化。

扫描线长度 * 两条相邻两条水平线的高度差 = 矩形面积

Up

void up(int o, int L, int R)
{
    if(cnt[o])
        len[o] = X[R + 1] - X[L];
    else if(L == R)
        len[o] = 0;
    else
        len[o] = len[o << 1] + len[o << 1 | 1];
}

这里按理说有if与else就行了，只是当L == R时不能按照else处理(叶子节点没有子节点了)，所以单独写一下。它等于0是因为这个不可分割的一段没有被覆盖，所以不取它。并不是因为什么“点没有长度”，这里线段树每个点也对应一段区间(不可再分割了)。

Code

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 210;

int n;

int num;
double X[N];
int cnt[N << 2 | 1];
double len[N << 2 | 1];

struct edge
{
    double l, r, h;
    int flag;
    edge(double a, double b, double c, int d):l(a), r(b), h(c), flag(d){}
    edge(){}
    bool operator < (const edge & t)const
    {
        return h < t.h;
    }
}e[N];

void up(int o, int L, int R)
{
    if(cnt[o])
        len[o] = X[R + 1] - X[L];
    else if(L == R)
        len[o] = 0;
    else
        len[o] = len[o << 1] + len[o << 1 | 1];
}

void update(int o, int L, int R, int l, int r, int val)
{
    if(L > r || R < l)
        return ;
    if(l <= L && R <= r)
    {
        cnt[o] += val;
        up(o, L, R);
        return ;
    }
    if(L == R)
        return ;

    int mid = (L + R) >> 1;
    update(o << 1, L, mid, l, r, val);
    update(o << 1 | 1, mid + 1, R, l, r, val);
    up(o, L, R);
}

int main()
{
    int t = 1;
    while(~scanf("%d", &n) && n)
    {
        num = 0;
        memset(len, 0, sizeof(len));
        memset(cnt, 0, sizeof(cnt));
        double a, b, c, d;
        for(int i = 0; i < n; ++i)
        {
            scanf("%lf %lf %lf %lf", &a, &b, &c, &d);
            X[num] = a;
            e[num++] = edge(a, c, b, 1);
            X[num] = c;
            e[num++] = edge(a, c, d, -1);
        }

        sort(e, e + num);
        sort(X, X + num);
        int m = unique(X, X + num) - X;

        double ans = 0;
        for(int i = 0; i < num; ++i)
        {
            int l = lower_bound(X, X + m, e[i].l) - X;///Segment Tree begins with 0
            int r = lower_bound(X, X + m, e[i].r) - X - 1;
            update(1, 0, m - 1, l, r, e[i].flag);
            ans += len[1] * (e[i + 1].h - e[i].h);
        }
        printf("Test case #%d\nTotal explored area: %.2f\n\n", t++, ans);
    }
    return 0;
}

离散化不仅有节省空间的作用，也可以将非整型数字对应到整型数字上方便进行线段树等操作的作用。

update左右子节点的时候，按理说需要把当前状态(cnt[o])down下去，但是up的设计使得down可忽略，而且cnt[o] += 1与cnt[o] += -1的成对存在保证了不出错。

而这一做法使得理论与实际有一定偏差，比如最开始那张图，到达第二条扫描线时设[1, 1]这个区间标号为o，则理论上cnt[o] = 2，因为他被覆盖了两次，而实际上cnt[o] = 1，还有个1在它父节点那儿，并没有down下来，而实际上这样做并不会出错（就是因为1与-1的成对存在）。

update函数中第一次up出现在“当前区间从属于目标区间”时刻，是因为这里的up并不是纯粹的up，纯粹的up是依据左右子节点的值更新len[o]：len[o] = len[o << 1] + len[o << 1 | 1];，也就是up中else那部分。这里的up应该是依据形参val更新len[o]，也就是up函数中if那部分。而之所以不分开写，是应为这两处同时需要他们俩。