HDU 4408 Minimun Spanning Tree (Count)

Description

最小生成树 + 生成树计数

Analyze

相对于普通的最小生成树，多了一个条件：最小，也就是说生成树的边有了权值。如果想办法去掉权值，问题就转为了普通生成树计数了。就像三维扫描线求体积那题，遍历Z轴，如同去掉了一个维度，将问题转化为了普通的扫描线求面积。这一题能不能通过遍历边的长度而将问题转化呢？可以的。

在Kruskal算法中：假设图中有a[1]条长度为b[1]的边，有a[2]条长度为b[2]的边…a[k]条长度为b[k]的边。这a[k]条长度相同的边的排列顺序可以是任意的，这意味着顺序不影响结果(即长度为b[k]的边被遍历过后形成的连通块是相同的，即缩点后的图是相同的)，也就是说在长度为b[k]的边的集合里，有num[k]个子集，选任意一个子集得到的结果都是相同的。这样一来，最终答案就是num[1] * num[2] *...*num[last]。

如何求num[k] ?

将长度小于b[k]的边都处理完(并查集unite)后形成一个个集合，这一个个集合相当于新图中的一个个“点”。这a[k]条长度为b[k]的边会使这些“点”形成一个个新的连通块，将每一个连通块看做一个图，Gauss计算生成树个数，每个连通块的生成树个数累乘就是num[k]。

Something

1.并查集需要用到一个记录祖先节点的数组，这里需要用到两个这样的数组F[]、K[]，K是F的将来，F是K的过去。在主函数里有如下代码：

u = found(F, e[i].u), v = found(F, e[i].v);
if(u != v)
{
    vis[u] = vis[v] = 1;
    K[ found(K, u) ] = found(K, v);
    A[u][v]++, A[v][u]++;
}

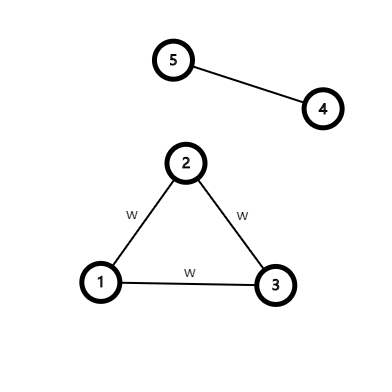
按照两个数组来，上面的环是会形成的，就可以正常进行生成树计数了。倘若只有一个数组，不可能形成环，若无环生成树个数只能是1。便是这里用到了两个数组，因为图的更新需要有“时差”。在此刻之前，K和F要同步。在此刻产生时差。在其他时刻，K和F没有合作关系。

Code

#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define ll long long
const int N = 105;
const int M = 1005;

ll ans, n, m, p;
ll A[N][N], C[N][N], F[N], K[N];
bool vis[N];
vector<ll> vec[N];

struct edge
{
    ll u, v, w;
    edge(ll a, ll b, ll c):u(a),v(b), w(c) {}
    edge() {}
    bool operator < (edge & t)const
    {
        return w < t.w;
    }
} e[M];

ll found(ll pre[], ll x)
{
    return pre[x] == x ? x : found(pre, pre[x]);
}

ll Gauss(ll cnt)
{
    ll res = 1;
    for(ll i = 0; i < cnt; ++i)
        for(ll j = 0; j < cnt; ++j)
            C[i][j] %= p;
    for(ll i = 0; i < cnt; ++i)
    {
        for(ll j = i + 1; j < cnt; ++j)
        {
            while(C[j][i])
            {
                ll t = C[i][i] / C[j][i];
                for(ll k = i; k < cnt; ++k)
                    C[i][k] = (C[i][k] - C[j][k] * t) % p;
                swap(C[i], C[j]);
                res = -res;
            }
        }
        if(C[i][i] == 0)
            return 0L;
        res = (res * C[i][i]) % p;
    }
    return (res + p) % p;
}

void Matrix_Tree()
{
    for(ll i = 0; i < n; ++i)
        if(vis[i])
            vec[ found(K, i) ].push_back(i), vis[i] = 0;

    for(ll i = 0; i < n; ++i)
        if(vec[i].size() > 1)
        {
            memset(C, 0, sizeof(C));
            ll len = vec[i].size();
            for(ll j = 0; j < len; ++j)
                for(ll k = j + 1; k < len; ++k)
                {
                    ll u = vec[i][j], v = vec[i][k];
                    if(A[u][v])
                    {
                        C[j][k] = C[k][j] -= A[u][v];
                        C[j][j] += A[u][v], C[k][k] += A[u][v];
                    }
                }

            ans = ans * Gauss(len - 1) % p;
            for(ll j = 0; j < len; ++j)
                F[ vec[i][j] ] = i;///Can't initial F[]/K[] with -1.
        }

    for(ll i = 0; i < n; ++i)
        vec[i].clear(), K[i] = F[i] = found(F, i);
}

int main()
{
    while(~scanf("%lld %lld %lld", &n, &m, &p) && n)
    {
        ll u, v, w;
        for(ll i = 0; i < m; ++i)
        {
            scanf("%lld %lld %lld", &u, &v, &w);
            u--, v--;
            e[i] = edge(u, v, w);
        }
        sort(e, e + m);

        ans = 1;
        memset(A, 0, sizeof(A));
        for(ll i = 0; i < n; ++i)
            K[i] = F[i] = i;
        for(ll i = 0; i <= m; ++i)
        {
            if(i && e[i].w != e[i - 1].w || i == m)
                Matrix_Tree();

            u = found(F, e[i].u), v = found(F, e[i].v);
            if(u != v)
            {
                vis[u] = vis[v] = 1;
                K[ found(K, u) ] = found(K, v);
                A[u][v]++, A[v][u]++;
            }
        }

        bool flag = 1;
        for(ll i = 1; i < n; ++i)
            if(F[i] != F[i - 1])
            {
                flag = 0;
                break;
            }

        printf("%lld\n", flag ? ans % p : 0);
    }
    return 0;
}

有人说路径压缩会影响点的度数什么的，进而影响邻接矩阵的正确性，故不能使用路径压缩，我想不明白，不过我试了一下路径压缩，也能AC。

还是不理解的地方

            for(ll j = 0; j < len; ++j)
                F[ vec[i][j] ] = i;///Can't initial F[]/K[] with -1.
        }

    for(ll i = 0; i < n; ++i)
        vec[i].clear(), K[i] = F[i] = found(F, i);
}

Matrix_Tree()函数里后一部分，这里(两个循环)是在更新，可是K不就是新图吗？把K拷贝给F不行吗？我试了不行。所以这算法我还有一个点没想明白，一个很大的、很重要的点！