HDU 4685 Prince and Princess(bipartite graph match and shrink nodes)

Description

N个王子M个公主，王子只能匹配自己喜欢的公主，公主随意。给出王子对于公主的喜爱信息，求在保证最大配对数的前提下，每个王子分别可以匹配哪些公主。

Analyze

为了保证最大匹配数，先对王子进行最大匹配(二分图匹配の匈牙利算法DFS)。

在最大匹配前提下，再找各王子除了匹配到的公主外还可以匹配哪些公主

遍历王子，对于没匹配公主的每个王子：

设置一个虚点(公主)与之匹配，并让所有王子指向这一虚点

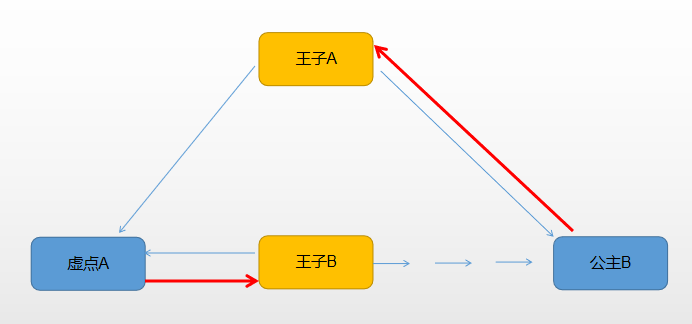
遍历公主，对于没匹配王子的每个公主：

设置一个虚点(王子)与之匹配，并让这一虚点指向所有公主

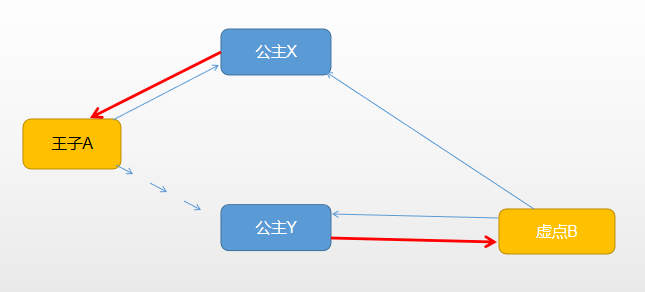
针对参与匹配的所有公主(最大匹配中的+虚点中的)，建立反向边

强连通分量缩点，处在同一个强连通分量中的王子与公主，可以彼此匹配

A遍历王子，love[A][B]==1用来排除B是王子(保证B是公主)

Code

#include <stack>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 2005;
const int M = 2 * N * N;
const int base = 500;

int n, m, ans[N];
bool love[N][N];

int head[N], cnt;
struct edge
{
    int v, pre;
} e[M];

void add(int u, int v)
{
    e[cnt].v = v;
    e[cnt].pre = head[u];
    head[u] = cnt++;
}

bool vis[N];
int girl[N], boy[N];
bool DFS(int x)
{
    for(int i = head[x]; ~i; i = e[i].pre)
    {
        int v = e[i].v;
        if(!vis[v])
        {
            vis[v] = 1;
            if(!girl[v] || DFS(girl[v]))
            {
                girl[v] = x;
                boy[x] = v;
                return 1;
            }
        }
    }
    return 0;
}

bool inst[N];
stack<int> st;
vector<int> scc[N];
int low[N], times[N], t, num, ltt[N];
void Tarjan(int x)
{
    st.push(x);
    inst[x] = 1;
    low[x] = times[x] = ++t;
    for(int i = head[x]; ~i; i = e[i].pre)
    {
        int to = e[i].v;
        if(!times[to])
        {
            Tarjan(to);
            low[x] = min(low[x], low[to]);
        }
        else if(inst[to])
            low[x] = min(low[x], times[to]);
    }

    if(low[x] == times[x])
    {
        ++num;
        while(!st.empty())
        {
            int tem = st.top();
            st.pop();
            ltt[tem] = num;
            inst[tem] = 0;

            if(tem > base && tem <= 2 * base)///This is a girl.
                scc[num].push_back(tem - base);

            if(tem == x)
                break;
        }
    }
}

void init()
{
    for(int i = 0; i <= num; ++i)
        scc[i].clear();
    cnt = t = num = 0;
    while(!st.empty())
        st.pop();
    memset(ltt, 0, sizeof(ltt));
    memset(boy, 0, sizeof(boy));
    memset(girl, 0, sizeof(girl));
    memset(love, 0, sizeof(love));
    memset(inst, 0, sizeof(inst));
    memset(head, -1, sizeof(head));
    memset(times, 0, sizeof(times));
}

///Prince : 1 ~ 500
///Princess : 501 ~ 1000
///Virtual nodes : 1001 ~ 2000
int main()
{
    int _, CASE = 1, tot = 0, v = 0;
    scanf("%d", &_);
    while(_--)
    {
        scanf("%d %d", &n, &m);

        init();
        for(int i = 1; i <= n; ++i)
        {
            scanf("%d", &tot);
            while(tot--)
            {
                scanf("%d", &v);
                love[i][v] = 1;
                add(i, base + v);
            }
        }

        ///Max match
        for(int i = 1; i <= n; ++i)
        {
            memset(vis, 0, sizeof(vis));
            DFS(i);
        }

        int node = 0;
        for(int i = 1; i <= n; ++i)
            if(!boy[i])
            {
                ++node;
                v = 2 * base + node;
                boy[i] = v, girl[v] = i;

                for(int j = 1; j <= n; ++j)
                    add(j, v);
            }
        for(int i = base + 1; i <= base + m; ++i)
            if(!girl[i])
            {
                ++node;
                v = 2 * base + node;
                girl[i] = v, boy[v] = i;

                for(int j = base + 1; j <= base + m; ++j)
                    add(v, j);
            }

        for(int i = base + 1; i <= base * 2 + node; ++i)
            add(i, girl[i]);

        for(int i = 1; i <= n; ++i)
            if(!times[i])
                Tarjan(i);

        printf("Case #%d:\n", CASE++);
        for(int i = 1; i <= n; ++i)
        {
            tot = 0;
            int sz = scc[ ltt[i] ].size();
            for(int j = 0; j < sz; ++j)
            {
                v = scc[ ltt[i] ][j];
                if(love[i][v])
                    ans[tot++] = v;
            }
            sort(ans, ans + tot);
            cout << tot;
            for(int j = 0; j < tot; ++j)
                printf(" %d", ans[j]);
            cout << '\n';
        }
    }
    return 0;
}

注意初始化顺序

void init()
{
    for(int i = 0; i <= num; ++i)
        scc[i].clear();
    cnt = t = num = 0;
}

因为没注意顺序，num先初始化为0，WA几个小时。